AI_逻辑回归(2)
逻辑回归
一:复杂的分类问题
1. 直线决策边界
通过 x1 和 x2 去判断 y的值
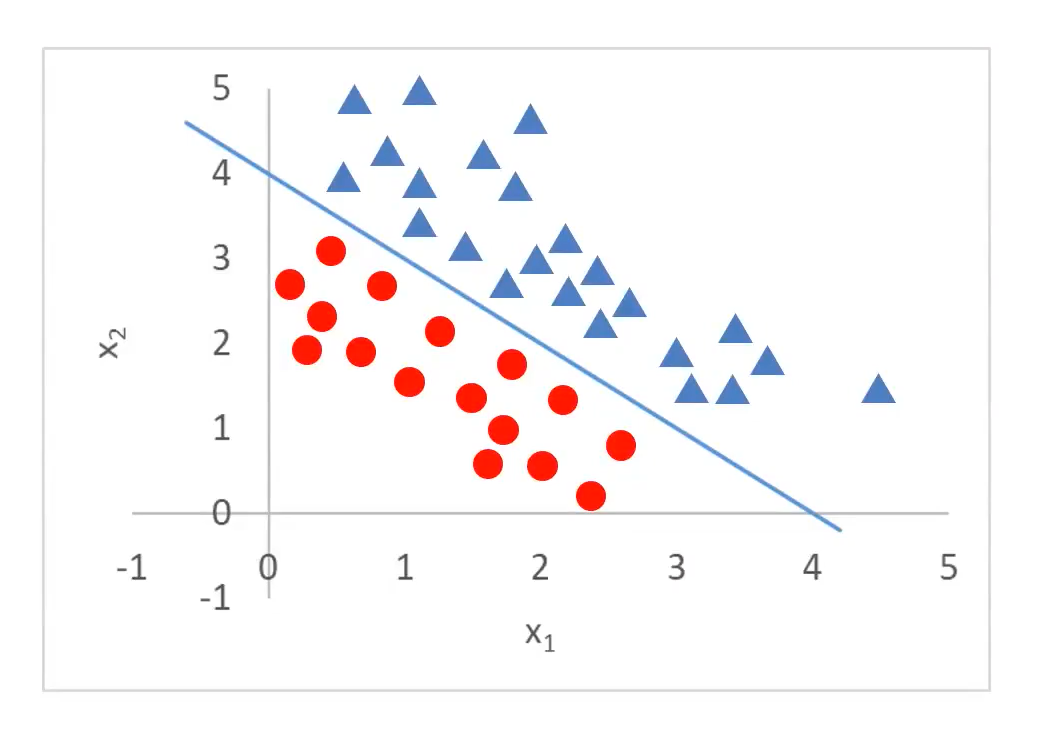
概念分布函数
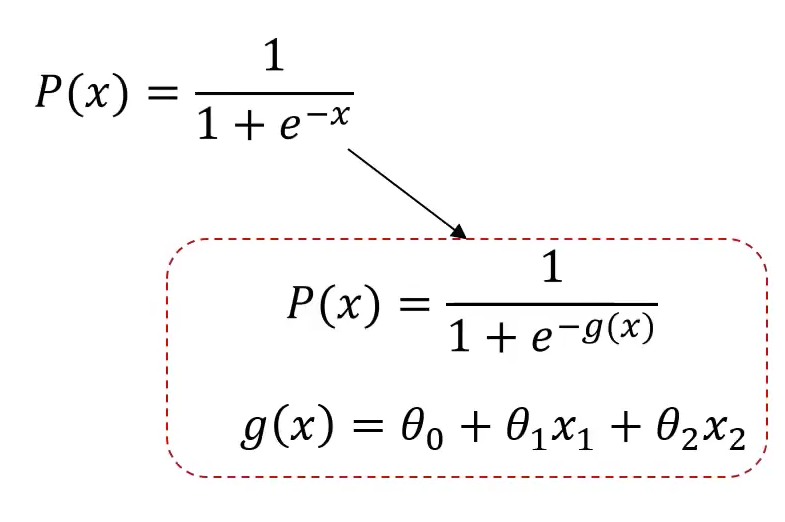
核心问题:找到 g(x),即蓝色的直线;
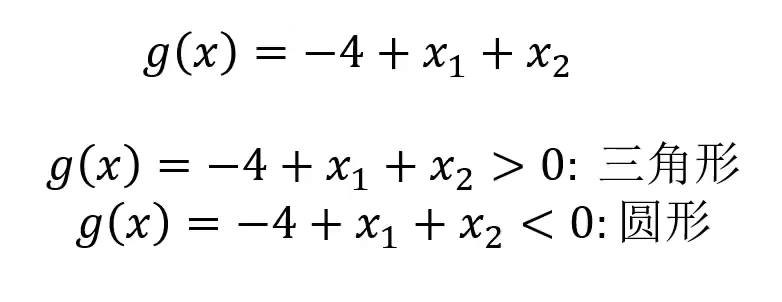
决策边界:

2. 圆形决策边界
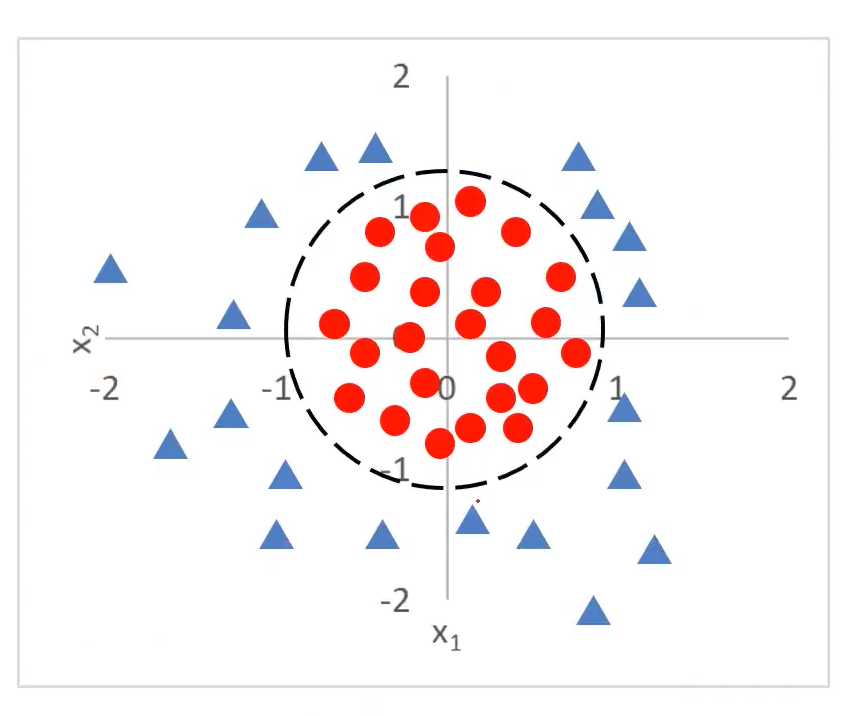
获取概念分布,逻辑回归方程:
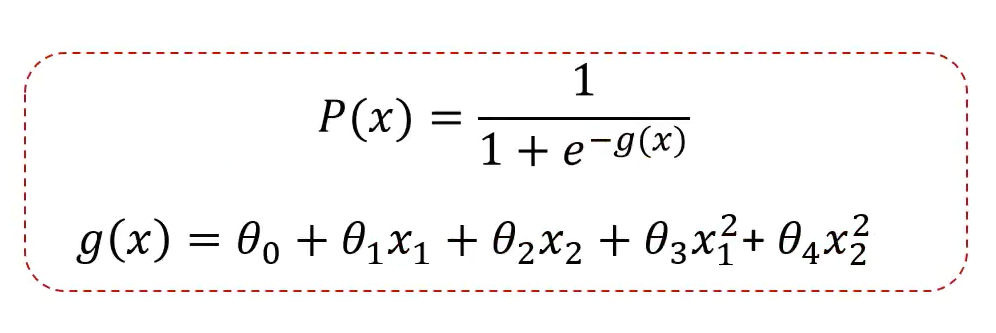
圆形的 g(x) 与直线的 g(x) 不同,新增了2此项。由此获取一个曲线或者圆形。
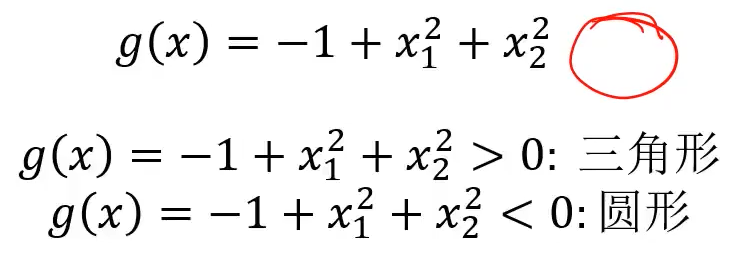
决策边界:
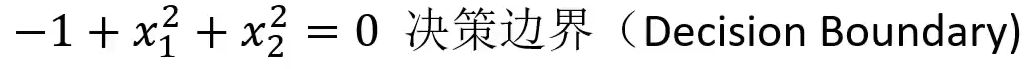
3. 总结
- 当使用逻辑回归去求解问题时,核心即找到决策边界。
- 逻辑回归结合多项式的边界函数,可以解决复杂的分类问题。
- 线性边界,即多项式为1次;
- 圆形边界,即多项式为2次;
二:逻辑回归问题求解
- 概念分布函数
- 对应的边界函数关系
1. 寻找类别边界
根据训练样本,寻找类别边界;
即:根据训练样本,寻找找 θ0、θ1、θ2
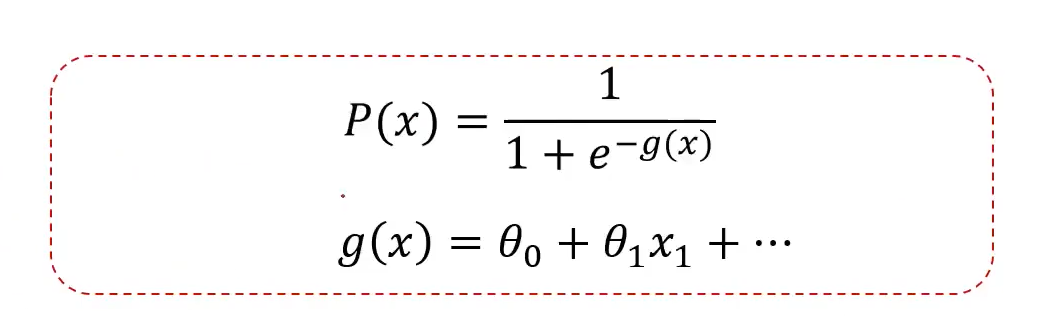
2. 如何求解系数

分类问题,标签与预测结果都是离散的点,使用该损失函数无法寻找到极小值点。

图像:
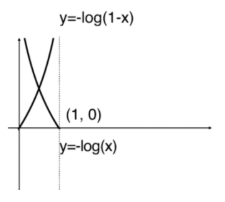
等效转换关系式:
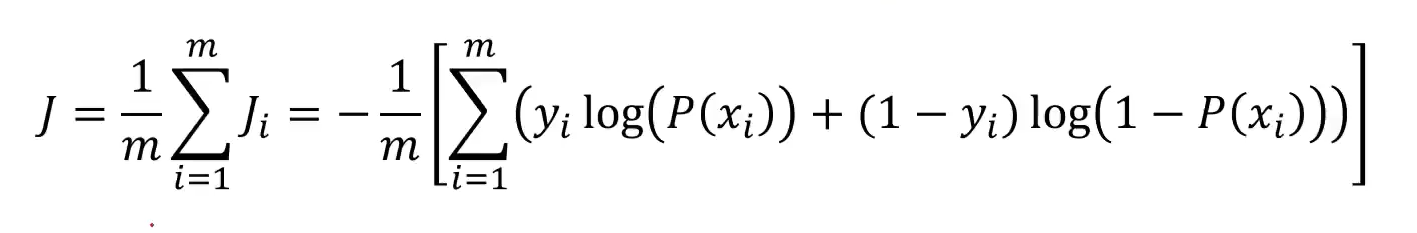
带入P(x),求解
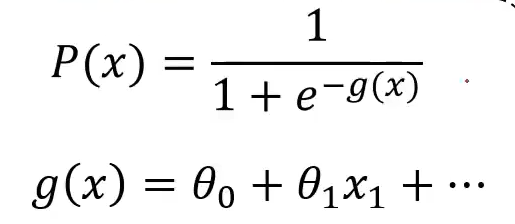
采用梯度下降法,获取最小化的损失函数 J
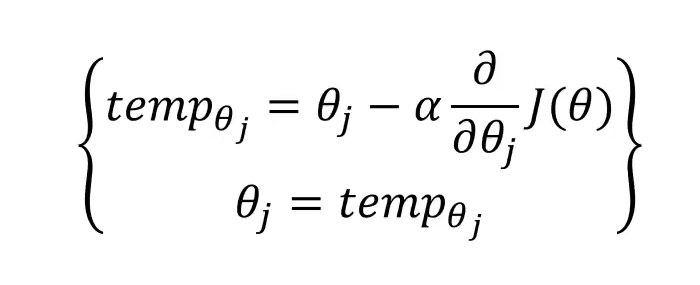
三:命名问题
逻辑回归的主要场景是分类问题,称其为逻辑回归是否合适,为什么?
逻辑回归虽然名字中有回归,但实际上它是一个二分类算法。
逻辑回归实际上就是在多元线性回归(θᵀx)的基础上,多嵌套了一个函数,这个函数就是 sigmoid 函数,也被称为 S 型曲线。
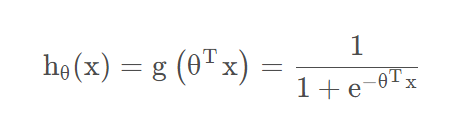
简化表达:
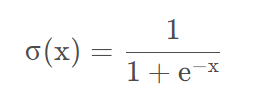
函数图像:
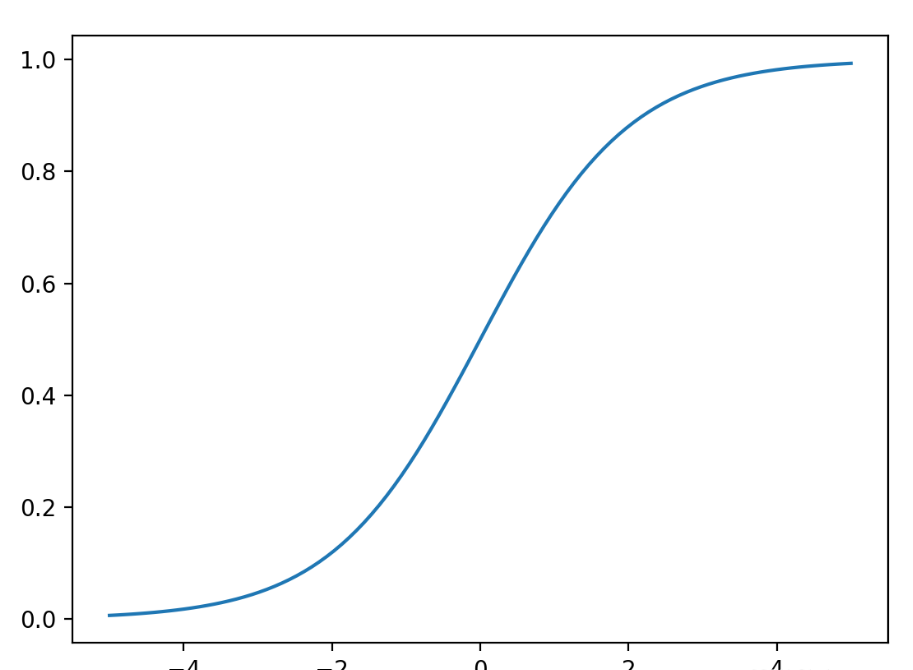
由 sigmoid 函数图像看知,其值域为(0,1)。因此逻辑回归就是在多元线性回归的基础上,讲结果缩放到了0 和 1 之间。
当我们通过线性函数得到一个结果,这个结果越小于0,函数输出就越接近0;结果越大于0,函数输出就越接近1,而分类算法的输出一般情况下都会是 input 属于某个类别的概念大小,因此用0到1之间的范围刚好可以表示概念。中间的0.5则将结果划分为两个类别。所以,我们可以简单的将 sigmoid 函数理解成一个将输出转化为属于某个类别的概念的函数。
综上所述,逻辑回归的大体思想就是,多元线性回归算法回归出一个分类超平面,预测样本通过代入这个超平面,如果是负就说明在这个超平面的下方,如果是正就说明是在这个超平面的上方。再通过 sigmoid 转换为概率,最好通过概率输出类别。
四:逻辑回归统计学模型:伯努利分布
我们知道,对于二分类算法,样本只有两个标签,要么是0要么是1,并且二分类有一个特点,那就是我们最终预测样本的概念,正例加上负例的概念总和是1。即每一次预测我们都可以这样表示:
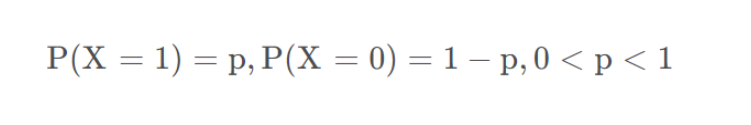
这个公式不就是伯努利分布(0-1分布)嘛!
因此,对于模型每一次预测的输出,我们都可以写成伯努利分布的形式:
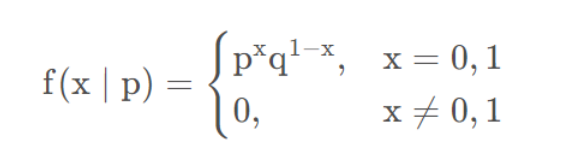
细微差异:
伯努利分布中,最经典的案例就是抛硬币。只不过在抛硬币前我们已经假设概率是对半分的。
但是在逻辑回归中,概念是需要通过每一次模型预测给出的。


